Обертоны и спектр

Французский математик Фурье (1768-1830) и его последователи доказали, что любое сложное колебание можно представить в виде суммы простейших колебаний, называемых собственными частотами, или, другими словами, что любую периодическую функцию, в случае ее соответствия некоторым математическим условиям, можно разложить в ряд (сумму) косинусов и синусов с некоторыми коэффициентами, называемый тригонометрическим рядом Фурье.

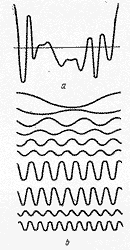Обертоном называется любая собственная частота выше первой, самой низкой ( основной тон ), а те обертоны, частоты которых относятся к частоте основного тона как целые числа, называются гармониками , причем основной тон считается первой гармоникой .

Если звук содержит в своем спектре только гармоники, то их сумма является периодическим процессом и звук дает четкое ощущение высоты. При этом субъективно ощущаемая высота звука соответствует наименьшему общему кратному частот гармоник.

Совокупность обертонов, составляющих сложный звук, называют спектром этого звука.

Разложение сложного звука на простейшие составляющие называют спектральным анализом , осуществляемым с помощью математического преобразования Фурье .

Методы спектрального анализа могут быть применены не только к периоди ческим сигналам, но также и к сигналам, представленным в цифровой форме . В зависимости от типа сигнала используются различные виды спектрального анализа: ряд Фурье (для периодических сигналов), интеграл Фурье (для непериодических сигналов), дискретное прео бразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ) для цифровых сигналов.

Периодический сигнал U ( t ) (например, звуковое давление или напряжение) должен удов летворять условию: U ( t ) = U ( t + nT ) где Т — период колебаний , n — це­ лое число.

Основная (фундаментальная) частота определяется как

Такой сигнал может быть представлен в виде ряда Фурье. т. е. в виде суммы гармоник:

Частоты этих гармонических составляющих равны:

Амплитуды этих составляющих определяются следующими формулами: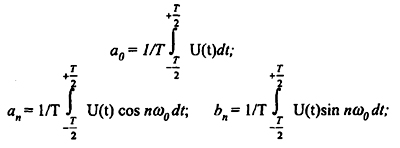
Ряд Фурье может быть записан и в другой форме: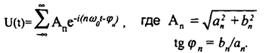

Как видно из этой формулы, любой сложный периодический звуковой сигнал может быть представлен в виде суммы простых гармонических сигналов с соответствующими ам плитудами и фазами. Сов окупность всех амплитуд на шкале частот называется амп литудным спектром, с овокуп­ ность всех фаз - фазовым спектром. При этом, несмотря на то, что ряд Фурье может быть бесконечным, предлагаемая им форма записи оказывается очень удобной при проведении анализа и обработки.

Так можно поступить с периодическими функциями. Однако и на практике, и в теории далеко не все функции периодические. Чтобы получить возможность раскладывать непериодическую функцию f(x) в ряд Фурье, можно воспользоваться "хитростью". Как правило, при рассмотрении некоторой сложной непериодической функции нас не интересуют ее значения на всей области определения; нам достаточно рассматривать функцию лишь на определенном конечном интервале [x1, x2] для некоторых x1 и x2. В этом случае функцию можно рассматривать как периодическую, с периодом Т = x2- x1. Для ее разложения в ряд Фурье на интервале [x1, x2] мы можем искусственно представить f(x) в виде некоторой периодической функции f'(x), полученной путем "зацикливания" значений функции f(x) из рассматриваемого интервала. После этой процедуры непериодическая функция f(x) превращается в периодическую f'(x), которая может быть разложена в ряд Фурье.

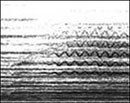
График, на котором изображен развернутый во времени спектр звука, называют спектральным представлением звука или сонограммой . Другими словами, сонограмма представляет собой диаграмму распределения спектральной энергии акустического источника в координатах частоты и времени. При этом по вертикали откладывают частоты обертонов, по горизонтали - время, а цвет (чаще всего оттенок серого), указывает на интенсивность обертонов.

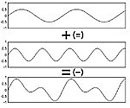Очевидно, что возможна обратная операция - конструирование сложного звука по его гармоническим составляющим - называемая синтезом Фурье или аддитивным синтезом, т.е. синтезом, основанным на принципе сложения . Другими словами, возможен синтез сложного звука из простейших синусоидальных тонов, частоты, амплитуды и фазы которых изменяются во времени по строго определенным законам. Своего рода виртуозом аддитивного синтеза был и остается французский композитор и пионер компьютерной музыки Жан Клод Риссе. Используют, также, и обратный метод: из сложного спектра с помощью специальных фильтров удаляют часть спектральных компонент, формируя желаемый тембр. Этот метод называют « субтрактивный синтез », т.е. синтез, основанный на принципе вычитания.